円弧の中点を求める

No.006 の延長として、円Ｏを分割して円弧を作ります。　円弧の端点をそれぞれＣ、Ｄとします。

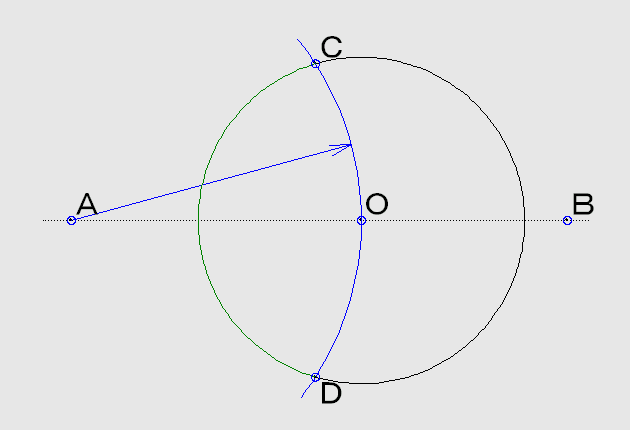
Ａを中心に半径ＯＡの円で切っていますが、これは適当でＯＫです。

Ｃ、Ｄを中心に、半径ＣＯ，ＤＯの円を描きます。　又、点Ｏを中心に半径ＣＤの円を描き、交点をＰ、Ｑとします。

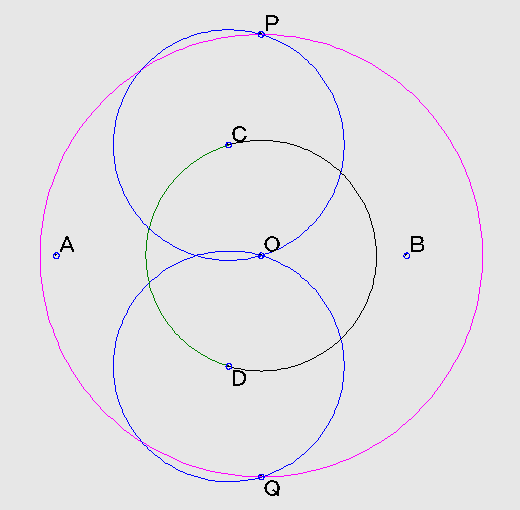
交点はＰ、Ｑの他に２点出来ますが、ここではＡの反対側を選択しています。

これが円ＡＯでカットした意味があります。　点Ｐ、Ｏ、Ｑは一直線上にあります。

尚、与えられた円弧で、交点が二つ（上下一つずつ）の時は、円弧は半円ですので、正方形作図を参考にして下さい。

点Ｐ、Ｑを中心に、それぞれ半径ＰＤ、ＱＣ（＝ＰＤ）の円を描き、交点をＲとします。

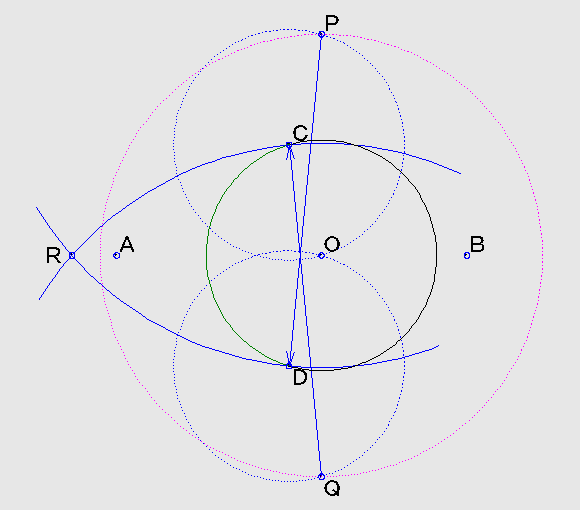
ここでは、交点はＡの側をつかっています。

最後に、点Ｐ（またはＱ）から、半径ＯＲの円を描いて交点を求めれば、これが円弧の中点になります。

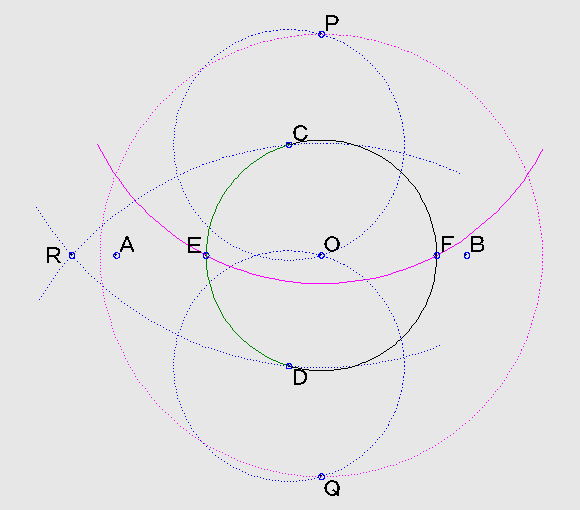
当然ながら、点Ｅ、Ｆは、直線ＡＢと円Ｏとの交点となっています。

証明は面倒くさいので省いてしまいました。　皆さん、挑戦してみて下さい。

dated 23 Nov., 2006