与えられた円の中心を求める

適当な所から適当な半径で円を描き、交点をＡとします（今後はこんな事は表記しませんが・・・）。

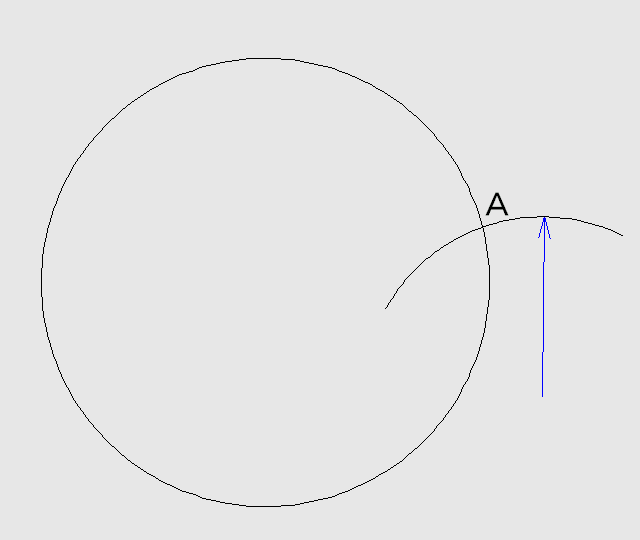
Ａを中心に適当な半径の円を描き、与えられた円との交点をＢ、Ｃとします。

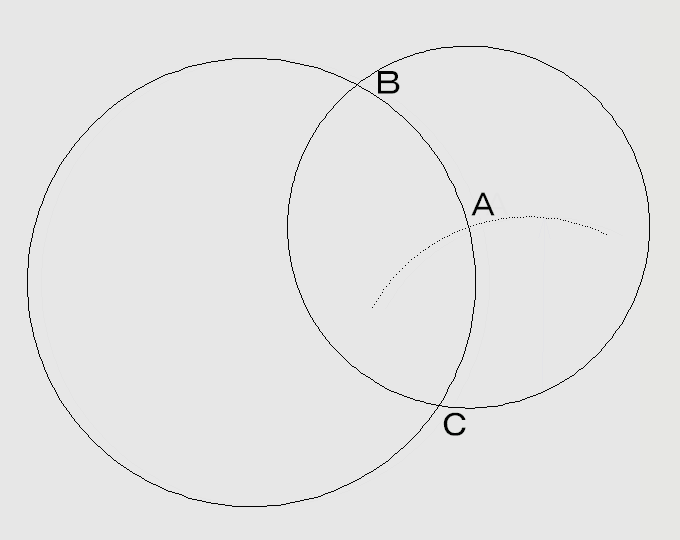
点Ｂ、Ｃを中心に半径ＢＡ（＝ＣＡ）の円を描き、Ａ以外の交点をＰとします。

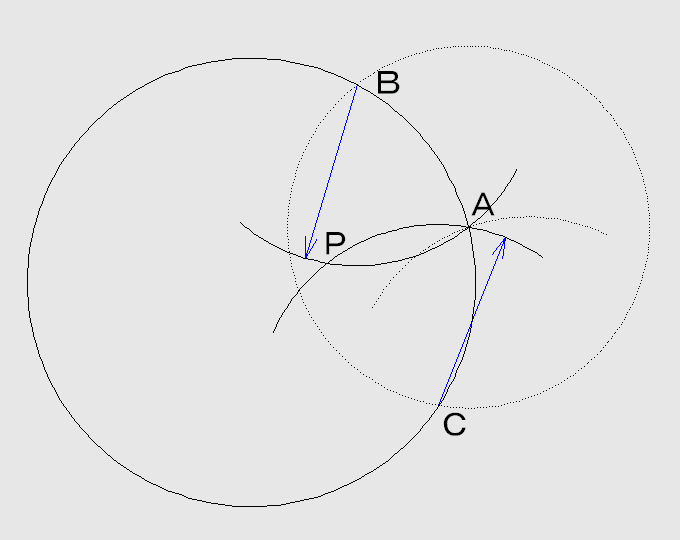
そうすると、与えられた円の半径をＲとすると、ＡＰ＝ＡＢ^２／Ｒとなります（相似の２等辺三角形）。

と言うことは、半径ＡＰの円とＡＢの円を使って、同じ作図をすればＲが得られる筈です（Ｒ＝ＡＢ^２／ＡＰだから）。

円ＰＡと円ＡＢとの交点をＢ’、Ｃ’とします（二つ上の図を参照して下さい。同じ事をしています）。

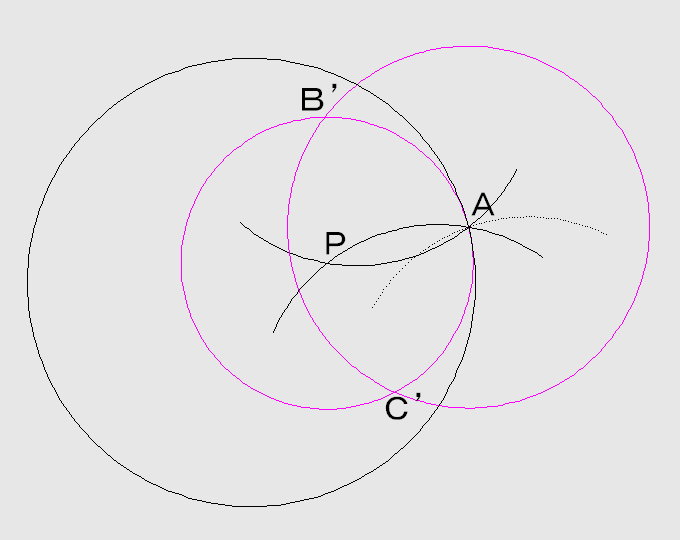
点Ｂ’、Ｃ’を中心に半径Ｂ’Ａ（＝Ｃ’Ａ）の円を描き、Ａ以外の交点をＯとすれば、これが求める中心です。

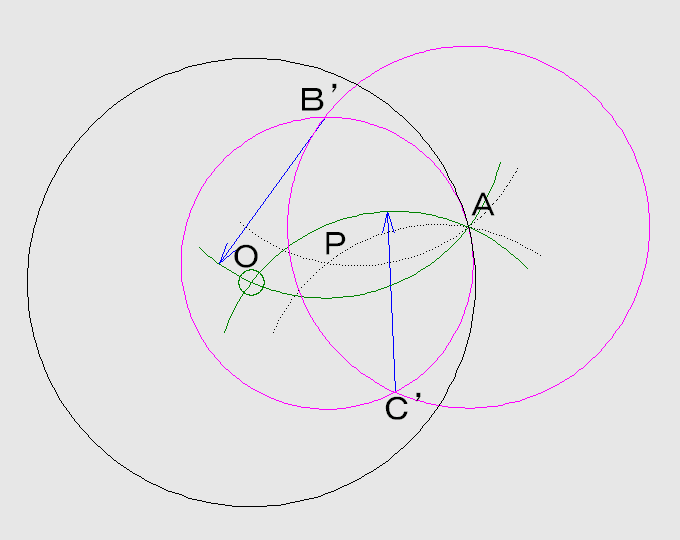
�凾oＡＢ’、�凾nＡＢ’は共に２等辺三角形で底角Ａが共通なので相似です。　後は省略します！

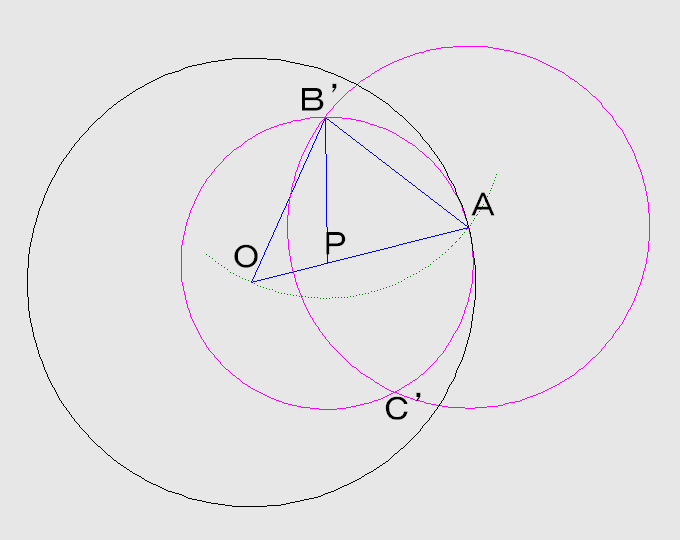
これは、定規とコンパスを使った作図より、線を描く回数が少ないですね！

この作図方法を見ればお判りの通り、円ではなく「弧」でも、その中心が見付かります。

dated 23 Nov., 2006